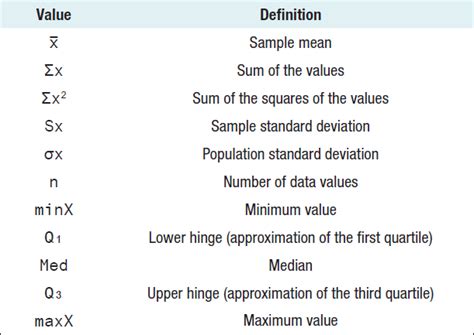
The realm of statistics is replete with a myriad of symbols, each carrying its own unique meaning and significance. One of the fundamental concepts in statistics is the variance, denoted by the symbol σ² (sigma squared) in population and s² in sample. The variance is a measure of the dispersion or spread of a set of data, indicating how much individual data points deviate from the mean value of the dataset.
Understanding Variance and Its Symbols

Variance is calculated as the average of the squared differences from the Mean. For a population, the formula is σ² = Σ(xi - μ)² / N, where xi represents each individual data point, μ is the population mean, and N is the total number of data points in the population. For a sample, the formula adjusts to s² = Σ(xi - x̄)² / (n - 1), where x̄ is the sample mean and n is the number of observations in the sample. The use of (n - 1) instead of n in the sample variance formula is known as Bessel’s correction, which helps to make the sample variance a more unbiased estimator of the population variance.
Interpreting Variance
A high variance indicates that the data points are spread out over a large range of values, whereas a low variance means that the data points tend to be closer to the mean. Variance is always positive or zero; it cannot be negative. A variance of zero means that all data points are exactly the same, indicating no variability at all. The square root of the variance, denoted by σ (sigma) for population and s for sample, is known as the standard deviation, which is also a measure of dispersion but is more interpretable because it is in the same units as the data.
| Statistic | Population Formula | Sample Formula |
|---|---|---|
| Variance | σ² = Σ(xi - μ)² / N | s² = Σ(xi - x̄)² / (n - 1) |
| Standard Deviation | σ = √(Σ(xi - μ)² / N) | s = √(Σ(xi - x̄)² / (n - 1)) |

Key Points
- Variance (σ² or s²) measures the dispersion of a dataset, indicating how much individual data points deviate from the mean.
- The standard deviation (σ or s) is the square root of the variance, providing a more interpretable measure of dispersion in the same units as the data.
- Population variance and standard deviation (σ² and σ) are used when the entire population is analyzed, whereas sample variance and standard deviation (s² and s) are used for sample data, with the sample formulas providing unbiased estimations of the population parameters.
- A high variance or standard deviation indicates a wide spread of data points, while a low value indicates that the data points are closer to the mean.
- Variance is always non-negative, with zero variance indicating no variation in the data.
Applying Variance in Real-World Scenarios

Variance has numerous applications across various fields, including finance, engineering, and social sciences. In finance, for instance, variance is used to measure the volatility of asset prices, helping investors assess the risk associated with different investments. In engineering, understanding the variance of a process or product characteristic is crucial for quality control and reliability analysis. In social sciences, variance can be used to analyze the spread of opinions or behaviors within a population.
Calculating Variance from Standard Deviation
If the standard deviation is known, the variance can be easily calculated by squaring the standard deviation. This is because variance is the square of the standard deviation (σ² = σ * σ or s² = s * s). This relationship makes it straightforward to move between these two measures of dispersion.
In conclusion, variance and its related symbols are fundamental components of statistical analysis, providing insights into the spread of data. Understanding variance is crucial for making informed decisions in various fields, from finance and engineering to social sciences and more. By grasping the concepts of variance and standard deviation, and knowing how to apply them, individuals can better analyze and interpret data, ultimately leading to more accurate predictions and better decision-making.
What is the difference between population and sample variance?
+The main difference between population and sample variance lies in their formulas and the context in which they are used. Population variance (σ²) uses the population mean (μ) and divides by the total number of data points (N), while sample variance (s²) uses the sample mean (x̄) and divides by (n - 1), where n is the sample size. This adjustment in sample variance helps to make it a more unbiased estimator of the population variance.
How do variance and standard deviation relate to each other?
+Variance and standard deviation are directly related; the standard deviation is the square root of the variance. If you know the variance, you can find the standard deviation by taking its square root, and vice versa, you can find the variance by squaring the standard deviation.
Why is variance important in statistical analysis?
+Variance is important because it measures the spread or dispersion of a dataset, which is crucial for understanding the nature of the data. It helps in assessing the risk, uncertainty, and variability within the data, making it a foundational concept in statistical analysis and decision-making across various disciplines.