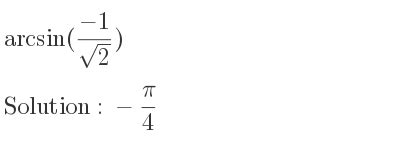The mathematical functions arcsin, 1, and sqrt(2) are fundamental components in trigonometry and calculus. To understand the relationship between these functions, we need to break down each component and then explore how they interact. The arcsin function, short for inverse sine, is used to determine the angle whose sine is a given number. The value 1 is a key input for the sine function, as sin(π/2) = 1. Lastly, sqrt(2) refers to the square root of 2, an irrational number approximately equal to 1.414.
Natural Language Explanation of Arcsin(1) and Its Relation to sqrt(2)

Arcsin(1) refers to the angle whose sine is 1. In a standard unit circle, this corresponds to 90 degrees or π/2 radians, because the sine of π/2 radians is 1. This is a straightforward calculation since sin(π/2) = 1, and therefore, arcsin(1) = π/2. On the other hand, the connection between arcsin(1) and sqrt(2) involves understanding the trigonometric identities and the geometric properties of right-angled triangles. For instance, in a right triangle with sides of equal length (an isosceles right triangle), the hypotenuse can be found using the Pythagorean theorem, which involves the square root of the sum of the squares of the other two sides. For a triangle with two sides of length 1, the hypotenuse’s length is sqrt(2), derived from sqrt(1^2 + 1^2) = sqrt(2).
Trigonometric Identity Involving Arcsin and sqrt(2)
One of the essential trigonometric identities involving the inverse sine function and sqrt(2) can be seen in the context of solving equations that involve these values. For example, if we consider the equation sin(x) = 1/sqrt(2), we’re looking for an angle whose sine is 1/sqrt(2). This is equivalent to arcsin(1/sqrt(2)). Knowing that sin(π/4) = 1/sqrt(2), we can infer that arcsin(1/sqrt(2)) = π/4. This example illustrates how arcsin and sqrt(2) can be related through trigonometric functions and identities, particularly in the context of right triangle trigonometry where angles and side lengths are intimately connected.
| Trigonometric Function | Input | Result |
|---|---|---|
| Arcsin | 1 | π/2 radians or 90 degrees |
| Sin | π/4 radians | 1/sqrt(2) |
| Sqrt | 2 | approximately 1.414 |

Key Points
- Arcsin(1) corresponds to the angle π/2 radians or 90 degrees because sin(π/2) = 1.
- Sqrt(2) is the length of the hypotenuse of a right triangle with two sides of length 1, derived from the Pythagorean theorem.
- The connection between arcsin and sqrt(2) is evident in trigonometric identities and the geometric properties of triangles, particularly in solving equations involving these values.
- Understanding these mathematical concepts and their relationships is crucial for solving problems in trigonometry, calculus, and physics.
- Arcsin(1/sqrt(2)) = π/4, illustrating how arcsin and sqrt(2) relate through specific trigonometric functions and identities.
In conclusion, the functions arcsin, the value 1, and sqrt(2) are intricately connected through trigonometric identities and geometric properties. Arcsin(1) gives us π/2 radians, reflecting the angle whose sine is 1, while sqrt(2) represents the length of the hypotenuse in an isosceles right triangle. These concepts and their relationships form the basis of more complex mathematical and physical analyses, demonstrating the beauty and coherence of mathematical principles.
What is the significance of arcsin(1) in trigonometry?
+Arcsin(1) signifies the angle whose sine is 1, which is π/2 radians or 90 degrees. This is a fundamental concept in trigonometry, relating to the unit circle and right-angled triangles.
How does sqrt(2) relate to right-angled triangles?
+Sqrt(2) is the length of the hypotenuse of a right triangle with two sides of equal length (1 unit), calculated using the Pythagorean theorem: sqrt(1^2 + 1^2) = sqrt(2).
What is the value of arcsin(1/sqrt(2))?
+Arcsin(1/sqrt(2)) equals π/4 radians, because the sine of π/4 radians is 1/sqrt(2). This relationship is essential in trigonometric calculations and identities.