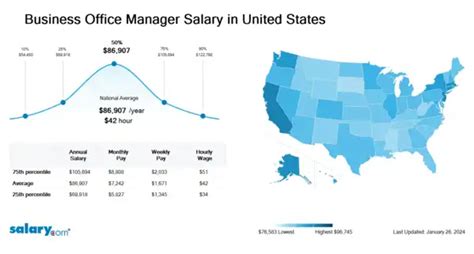
Understanding how to find common factors between two numbers is a fundamental concept in mathematics, essential for various applications, including algebra, geometry, and number theory. In this article, we'll explore the process of finding the common factors of 8 and 12, breaking down the steps for easy comprehension.
To begin with, let's define what factors are. Factors are the numbers that can be multiplied together to get a specific number. For instance, the factors of 8 are 1, 2, 4, and 8, because 1*8 = 8, 2*4 = 8. Similarly, the factors of 12 are 1, 2, 3, 4, 6, and 12, because 1*12 = 12, 2*6 = 12, and 3*4 = 12.
Listing Factors for 8 and 12
To find the common factors of 8 and 12, we first list all the factors for each number.
The factors of 8 are: 1, 2, 4, 8.
The factors of 12 are: 1, 2, 3, 4, 6, 12.
Identifying Common Factors
Now, we compare the lists of factors for 8 and 12 to identify the numbers that appear in both lists.
Comparing the factors: - The factors of 8 are: 1, 2, 4, 8. - The factors of 12 are: 1, 2, 3, 4, 6, 12.
We notice that 1, 2, and 4 appear in both lists.
Determining the Greatest Common Factor (GCF)
Among the common factors, it's often useful to identify the greatest one, known as the Greatest Common Factor (GCF). The GCF of 8 and 12 is 4, because 4 is the largest number that divides both 8 and 12 without leaving a remainder.
Key Points
- The factors of 8 are 1, 2, 4, and 8.
- The factors of 12 are 1, 2, 3, 4, 6, and 12.
- The common factors of 8 and 12 are 1, 2, and 4.
- The Greatest Common Factor (GCF) of 8 and 12 is 4.
- Understanding common factors is crucial for simplifying fractions, solving equations, and working with ratios.
Methodological Approaches
There are multiple methods to find common factors, including:
- Listing factors, as demonstrated above.
- Using prime factorization: Breaking down each number into its prime factors and then identifying common factors.
- Euclidean algorithm: A systematic approach to find the GCF of two numbers.
For 8 and 12, the prime factorization method works as follows:
The prime factorization of 8 is 2^3.
The prime factorization of 12 is 2^2 * 3.
The common prime factor is 2. The lowest power of 2 they share is 2^2 = 4, confirming that 4 is the GCF.
| Method | Description |
|---|---|
| Listing Factors | Directly listing all factors for each number and comparing. |
| Prime Factorization | Breaking down numbers into prime factors and finding common factors. |
| Euclidean Algorithm | A step-by-step method to find the GCF. |
Real-World Applications
Finding common factors has practical applications in real-life scenarios, such as:
1. Recipe Adjustments: When adjusting recipes, you might need to find common factors to scale ingredients up or down.
2. Financial Planning: In finance, understanding common factors can help in budgeting and financial forecasting.
3. Design and Architecture: Common factors are used in design to ensure symmetry and balance.
What are factors in mathematics?
+Factors are numbers that can be multiplied together to get a specific number. For example, the factors of 6 are 1, 2, 3, and 6.
How do you find the common factors of two numbers?
+To find the common factors, list all the factors for each number and then identify the numbers that appear in both lists.
What is the Greatest Common Factor (GCF)?
+The GCF is the largest number that divides two or more numbers without leaving a remainder. For 8 and 12, the GCF is 4.
In conclusion, finding the common factors of 8 and 12, or any two numbers, involves listing their factors and identifying the shared ones. This fundamental concept in mathematics has wide-ranging applications and is crucial for building a strong foundation in number theory and algebra.