The concept of log base 2, denoted as log2(x), is a fundamental mathematical operation that has numerous applications across various fields, including computer science, mathematics, and engineering. Log2(x) represents the power to which the base number 2 must be raised to produce the number x. In this article, we will explore five distinct ways to calculate log2(x), each with its own set of advantages and applications.
Key Points
- Understanding the concept of log base 2 and its importance in various fields
- Calculating log2(x) using mathematical properties and logarithmic identities
- Utilizing computational methods and algorithms for log2(x) calculation
- Exploring the relationship between log2(x) and other mathematical operations
- Applying log2(x) in real-world scenarios and problem-solving
Mathematical Properties and Logarithmic Identities

One of the primary methods for calculating log2(x) involves utilizing mathematical properties and logarithmic identities. The logarithm of a number to a certain base can be expressed in terms of its logarithm to another base, using the change of base formula: log2(x) = ln(x) / ln(2), where ln represents the natural logarithm. This method allows for the calculation of log2(x) using the natural logarithm, which is often readily available in mathematical libraries and calculators.
Computational Methods and Algorithms
Another approach to calculating log2(x) involves the use of computational methods and algorithms. One such method is the iterative calculation of log2(x) using the formula: log2(x) = log2(x/2) + 1, for x ≥ 2. This method can be repeated until the desired level of precision is achieved. Additionally, algorithms such as the binary search algorithm can be employed to find the integer part of log2(x), followed by interpolation to obtain the fractional part.
| Method | Description | Example |
|---|---|---|
| Mathematical Properties | Utilizing logarithmic identities and change of base formula | log2(8) = ln(8) / ln(2) = 3 |
| Computational Methods | Iterative calculation and binary search algorithm | log2(10) ≈ 3.322 (using iterative calculation) |
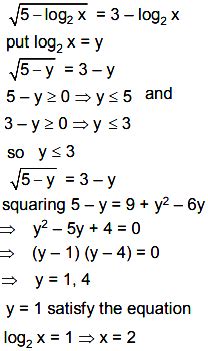
Relationship with Other Mathematical Operations
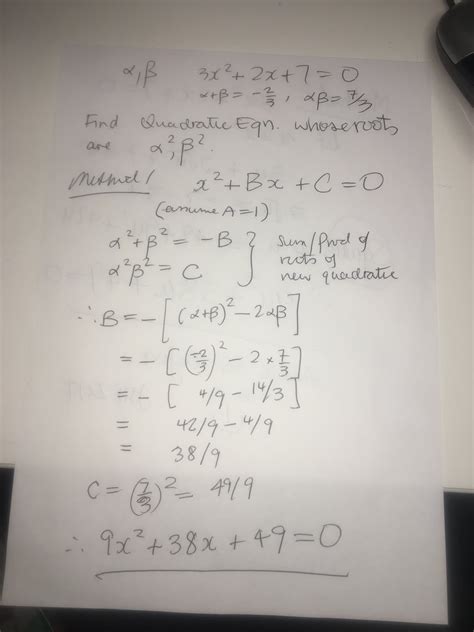
Log2(x) is closely related to other mathematical operations, such as exponentiation and roots. The logarithm and exponential functions are inverses of each other, meaning that log2(x) and 2^x are inverse operations. This relationship can be exploited to calculate log2(x) using exponentiation, as in the case of the iterative calculation method. Furthermore, the logarithm can be used to simplify complex expressions involving roots and exponents.
Real-World Applications and Problem-Solving
Log2(x) has numerous real-world applications, including data compression, cryptography, and algorithm analysis. In data compression, log2(x) is used to calculate the entropy of a dataset, which measures the amount of information contained in the data. In cryptography, log2(x) is used to calculate the strength of a cryptographic key, which determines the level of security provided by the key. Understanding log2(x) and its applications is essential for developing efficient algorithms and solving complex problems in these fields.
What is the difference between log2(x) and ln(x)?
+Log2(x) is the logarithm of x to the base 2, while ln(x) is the natural logarithm of x, which is the logarithm to the base e (approximately 2.718). The two logarithms differ in their base and are related by the change of base formula: log2(x) = ln(x) / ln(2).
How is log2(x) used in computer science?
+Log2(x) is used in computer science to analyze the time and space complexity of algorithms, as well as to calculate the entropy of data. It is also used in data compression, cryptography, and other applications where the logarithm is essential for efficient computation.
Can log2(x) be calculated using a calculator?
+Yes, log2(x) can be calculated using a calculator that supports logarithmic functions. Many calculators have a built-in log2(x) function or allow the user to calculate it using the change of base formula and the natural logarithm function.
In conclusion, log2(x) is a fundamental mathematical operation with numerous applications across various fields. Understanding the different methods for calculating log2(x), including mathematical properties, computational methods, and algorithms, is essential for selecting the most suitable approach for a given problem. By exploring the relationship between log2(x) and other mathematical operations, as well as its real-world applications, we can gain a deeper appreciation for the importance of this operation in modern mathematics and computer science.