The concept of training a model using a link function is a fundamental aspect of generalized linear models (GLMs) in statistics. A link function is a mathematical function that connects the expected value of a response variable to the linear predictor, which is a linear combination of predictor variables. This connection enables the modeling of non-normal response variables, such as binary or count data, by transforming the expected response into a continuous, unbounded variable that can be modeled using linear regression techniques.
Understanding Link Functions

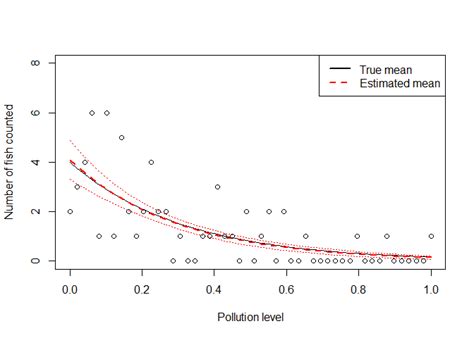
Link functions play a crucial role in extending the capabilities of linear regression to a broader range of data types. For instance, in logistic regression, which is used for binary classification problems, the logit link function is applied. This function maps the probability of an event occurring (a value between 0 and 1) to the entire real number line, allowing for the use of linear modeling techniques. Similarly, for count data, the log link function is often used, transforming the expected count into a continuous variable that can be modeled linearly.
Types of Link Functions
Several types of link functions are used in GLMs, each suited to different types of response variables:
- Logit Link Function: Used in logistic regression for binary response variables, it maps probabilities to the real number line.
- Log Link Function: Applied to count data, it transforms the expected count into a continuous variable.
- Probit Link Function: Similar to the logit link, but used in probit regression, it is based on the cumulative distribution function of the standard normal distribution.
- Identity Link Function: Used for continuous response variables, it leaves the expected response unchanged, essentially reducing the GLM to a traditional linear regression model.
| Type of Response Variable | Appropriate Link Function |
|---|---|
| Binary | Logit or Probit |
| Count | Log |
| Continuous | Identity |
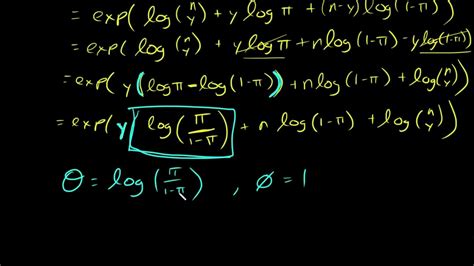
Training the Model
Training a GLM involves estimating the parameters of the linear predictor and the link function that best fit the observed data. This is typically achieved through maximum likelihood estimation (MLE), where the goal is to find the parameters that maximize the likelihood of observing the data given the model. The process involves:
- Specifying the Model: Choosing the link function and the linear predictor based on the type of response variable and the research question.
- Estimating Parameters: Using MLE to find the best-fitting parameters for the model.
- Evaluating the Model: Assessing the model’s fit and predictive performance using various metrics and diagnostic plots.
Key Points
- Link functions are essential for modeling non-normal response variables in GLMs.
- The choice of link function depends on the type of response variable.
- Maximum likelihood estimation is commonly used for parameter estimation in GLMs.
- Model evaluation is crucial for ensuring the model's accuracy and reliability.
- Understanding the underlying assumptions of GLMs and link functions is vital for correct model specification and interpretation.
Common Applications
- Medicine: Logistic regression for predicting disease risk based on patient characteristics.
- Marketing: Using logistic regression to predict customer churn or purchase likelihood.
- Environmental Science: Modeling count data, such as the number of species in an area, using Poisson regression with a log link function.
In conclusion, the use of link functions in GLMs provides a powerful framework for analyzing and modeling a variety of response variables. By understanding the role of link functions and how to select and apply them appropriately, researchers and practitioners can develop more accurate and informative models that better capture the underlying relationships in their data.
What is the primary purpose of a link function in generalized linear models?
+The primary purpose of a link function is to establish a relationship between the expected value of the response variable and the linear predictor, allowing for the modeling of non-normal response variables.
How do you choose the appropriate link function for a generalized linear model?
+The choice of link function depends on the type of response variable. For example, the logit link function is used for binary response variables, while the log link function is used for count data.
What is the role of maximum likelihood estimation in training a generalized linear model?
+Maximum likelihood estimation is used to find the parameters of the model that maximize the likelihood of observing the data given the model, essentially providing the best fit of the model to the data.