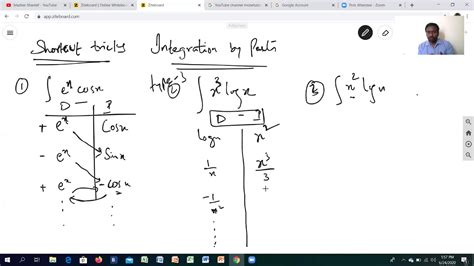
The concept of integration is a cornerstone of various fields, including mathematics, physics, and engineering. In a broader sense, integration refers to the process of combining different components or systems to create a unified whole. In this article, we will explore five ways integration can be applied across different domains, highlighting its significance and versatility.
Key Points
- Integration is a fundamental concept in mathematics, enabling the calculation of areas, volumes, and other quantities.
- In physics, integration is used to describe the motion of objects, energy transfer, and the behavior of complex systems.
- Engineering applications of integration include the design of electronic circuits, mechanical systems, and structural analysis.
- Integration is also crucial in data analysis, allowing for the combination of different data sources and the identification of trends.
- In a business context, integration refers to the process of combining different departments, systems, or companies to create a more efficient and effective organization.
Mathematical Integration

Mathematical integration is a fundamental concept in calculus, which deals with the study of continuous change. It is used to calculate the area under curves, volumes of solids, and other quantities. There are two main types of integration: definite and indefinite. Definite integration involves finding the area between a curve and the x-axis within a specific interval, whereas indefinite integration involves finding the antiderivative of a function. Integration is a powerful tool for solving problems in physics, engineering, and economics.
Applications of Mathematical Integration
Mathematical integration has numerous applications in various fields. In physics, it is used to describe the motion of objects, including the calculation of distances, velocities, and accelerations. In engineering, integration is used to design electronic circuits, mechanical systems, and structural analysis. For instance, integration is used to calculate the stress and strain on materials, ensuring that buildings and bridges can withstand various loads and stresses.
| Type of Integration | Description |
|---|---|
| Definite Integration | Calculates the area between a curve and the x-axis within a specific interval |
| Indefinite Integration | Finds the antiderivative of a function |
Physical Integration

Physical integration refers to the process of combining different physical systems or components to create a unified whole. In physics, integration is used to describe the motion of objects, energy transfer, and the behavior of complex systems. For example, integration is used to calculate the trajectory of projectiles, the motion of pendulums, and the behavior of electrical circuits.
Applications of Physical Integration
Physical integration has numerous applications in various fields, including engineering, materials science, and biophysics. In engineering, integration is used to design and optimize systems, such as electronic circuits, mechanical systems, and structural analysis. In materials science, integration is used to study the properties of materials, including their strength, conductivity, and optical properties.
Engineering Integration
Engineering integration refers to the process of combining different engineering disciplines to create a unified whole. This includes the integration of mechanical, electrical, and software engineering to design and develop complex systems, such as robots, autonomous vehicles, and medical devices. Engineering integration is critical for the development of innovative solutions to complex problems and the creation of more efficient systems.
Applications of Engineering Integration
Engineering integration has numerous applications in various fields, including aerospace, automotive, and biomedical engineering. In aerospace engineering, integration is used to design and develop complex systems, such as spacecraft, aircraft, and satellites. In automotive engineering, integration is used to design and develop vehicles, including their mechanical, electrical, and software systems.
Data Integration
Data integration refers to the process of combining different data sources to create a unified whole. This includes the integration of structured and unstructured data, such as databases, spreadsheets, and text files. Data integration is critical for businesses and organizations, as it enables them to make informed decisions, identify trends, and optimize their operations.
Applications of Data Integration
Data integration has numerous applications in various fields, including business intelligence, data analytics, and machine learning. In business intelligence, integration is used to combine data from different sources, such as customer relationship management (CRM) systems, enterprise resource planning (ERP) systems, and supply chain management (SCM) systems. In data analytics, integration is used to identify trends, patterns, and correlations in large datasets.
Business Integration
Business integration refers to the process of combining different departments, systems, or companies to create a more efficient and effective organization. This includes the integration of business processes, such as sales, marketing, and customer service, as well as the integration of different business functions, such as finance, human resources, and operations. Business integration is critical for organizations, as it enables them to respond to changing market conditions, improve their competitiveness, and increase their profitability.
Applications of Business Integration
Business integration has numerous applications in various fields, including management, marketing, and finance. In management, integration is used to combine different business functions, such as strategy, operations, and human resources, to create a more efficient and effective organization. In marketing, integration is used to combine different marketing channels, such as social media, email, and advertising, to create a more effective marketing strategy.
What is the main difference between definite and indefinite integration?
+Definite integration involves finding the area between a curve and the x-axis within a specific interval, whereas indefinite integration involves finding the antiderivative of a function.
How is integration used in physics?
+Integration is used in physics to describe the motion of objects, energy transfer, and the behavior of complex systems. It is used to calculate the trajectory of projectiles, the motion of pendulums, and the behavior of electrical circuits.
What are the benefits of business integration?
+Business integration enables organizations to respond to changing market conditions, improve their competitiveness, and increase their profitability. It also enables them to make informed decisions, identify trends, and optimize their operations.
In conclusion, integration is a fundamental concept that has numerous applications in various fields, including mathematics, physics, engineering, data analysis, and business. By understanding the principles of integration, professionals can develop innovative solutions to complex problems and create more efficient systems. Whether it is mathematical integration, physical integration, engineering integration, data integration, or business integration, the concept of integration is critical for creating a unified whole and achieving success in various endeavors.