Python, with its extensive libraries and simplicity, has become a go-to language for various graph-related operations, including finding connected components in a graph. Connected components are subgraphs in which there is a path between any two vertices. Understanding and identifying these components is crucial in network analysis, clustering, and more. Here are 5 tips for working with connected components in Python, along with examples and explanations to guide you through the process.
Understanding Connected Components

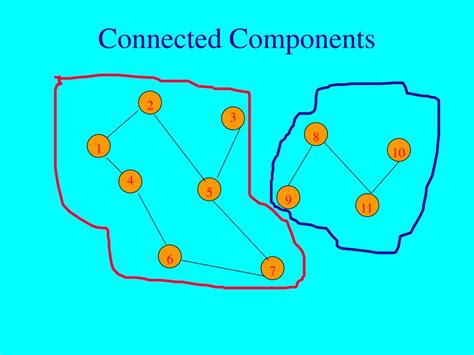
Before diving into the tips, it’s essential to grasp what connected components are. In the context of graph theory, a connected component of an undirected graph is a subgraph in which any two vertices are connected to each other by paths, and which is connected to no additional vertices in the supergraph. For directed graphs, the concept is slightly different, focusing on strongly connected components where there is a path from every vertex to every other vertex in the subgraph.
Tip 1: Choosing the Right Library
Python offers several libraries for graph operations, including NetworkX, igraph, and graph-tool. Among these, NetworkX is one of the most popular and user-friendly libraries for handling graphs and finding connected components. You can install it using pip: pip install networkx. For example, to find connected components in an undirected graph, you can use the connected_components function provided by NetworkX.
import networkx as nx
import matplotlib.pyplot as plt
# Create an empty graph
G = nx.Graph()
# Add edges
G.add_edge(1, 2)
G.add_edge(2, 3)
G.add_edge(3, 1)
G.add_edge(4, 5)
# Find connected components
components = list(nx.connected_components(G))
# Print components
for i, component in enumerate(components):
print(f"Component {i+1}: {component}")
Identifying Strongly Connected Components
In directed graphs, the concept of strongly connected components (SCCs) becomes relevant. An SCC is a subgraph that has a path from every vertex to every other vertex. NetworkX provides the strongly_connected_components function to find these components.
Tip 2: Visualizing Connected Components
Visualizing connected components can help in understanding the structure of the graph. NetworkX, in combination with matplotlib, allows you to draw graphs and highlight connected components. You can color nodes based on their component membership for better visualization.
import networkx as nx
import matplotlib.pyplot as plt
# Create a graph
G = nx.Graph()
G.add_edge(1, 2)
G.add_edge(2, 3)
G.add_edge(3, 1)
G.add_edge(4, 5)
# Find connected components
components = list(nx.connected_components(G))
# Color nodes by component
color_map = []
for node in G.nodes():
for i, component in enumerate(components):
if node in component:
color_map.append(i)
# Draw the graph
nx.draw(G, node_color=color_map, cmap=plt.cm.tab20)
plt.show()
Tip 3: Handling Large Graphs
For very large graphs, finding connected components can be computationally intensive. In such cases, optimizing the graph representation (e.g., using sparse matrices) and leveraging more efficient algorithms can help. Libraries like graph-tool provide efficient implementations for large-scale graph analysis.
Efficient Algorithms
The choice of algorithm can significantly impact performance. For instance, Tarjan’s algorithm for finding strongly connected components in a directed graph is more efficient than a brute-force approach. Understanding the time complexity of different algorithms and choosing the one that best fits your graph’s characteristics can lead to substantial performance improvements.
Tip 4: Understanding Algorithmic Complexity
Knowing the time and space complexity of the algorithms you’re using is crucial. For example, NetworkX’s connected_components function has a time complexity of O(V + E), where V is the number of vertices, and E is the number of edges, making it efficient for large graphs. Always consider the scalability of your solution.
Tip 5: Practical Applications
Connected components have numerous practical applications, including web page grouping, social network analysis, and cluster identification in data sets. By applying connected component analysis, you can gain insights into the structure and organization of complex systems.
| Application Area | Description |
|---|---|
| Web Graph Analysis | Identifying clusters of densely connected web pages. |
| Social Network Analysis | Finding communities or groups within social networks. |
| Data Clustering | Grouping similar data points based on their connectivity. |
Key Points
- Choose the right library based on your specific needs, with NetworkX being a versatile option for most graph operations.
- Understand the difference between connected components in undirected graphs and strongly connected components in directed graphs.
- Visualizing connected components can provide valuable insights into the graph's structure.
- Optimize your approach for large graphs by considering algorithmic complexity and efficient data structures.
- Connected component analysis has numerous practical applications across various fields, including web analysis, social networks, and data clustering.
In conclusion, working with connected components in Python involves choosing the right tools, understanding graph theory concepts, optimizing for performance, and applying these insights to real-world problems. By following these tips and continuously exploring the capabilities of libraries like NetworkX, you can effectively analyze and understand the structure of complex networks.
What is the difference between a connected component and a strongly connected component?
+A connected component is a subgraph where there is a path between any two vertices in an undirected graph. A strongly connected component, relevant to directed graphs, requires a path from every vertex to every other vertex within the subgraph.
How do I visualize connected components in a graph using Python?
+You can visualize connected components using NetworkX in combination with matplotlib. Assign a different color to nodes based on their component membership and then draw the graph using these colors.
What are some practical applications of connected component analysis?
+Connected component analysis has applications in web graph analysis, social network analysis, data clustering, and more. It helps in identifying groups or communities within large networks.