An optimizer is a system, process, or tool designed to improve the performance, efficiency, or effectiveness of a particular task, process, or system. Optimizers can be found in various fields, including computer science, engineering, economics, and mathematics. The primary goal of an optimizer is to find the best possible solution or configuration that maximizes or minimizes a specific objective function, subject to certain constraints and limitations.
Types of Optimizers
There are several types of optimizers, including:
- Linear Programming (LP) Optimizers: used to solve linear optimization problems, where the objective function and constraints are linear.
- Non-Linear Programming (NLP) Optimizers: used to solve non-linear optimization problems, where the objective function or constraints are non-linear.
- Integer Programming (IP) Optimizers: used to solve optimization problems where some or all of the variables are integers.
- Dynamic Programming (DP) Optimizers: used to solve optimization problems that have overlapping subproblems or that can be broken down into smaller subproblems.
- Stochastic Optimizers: used to solve optimization problems that involve uncertainty or randomness.
How Optimizers Work
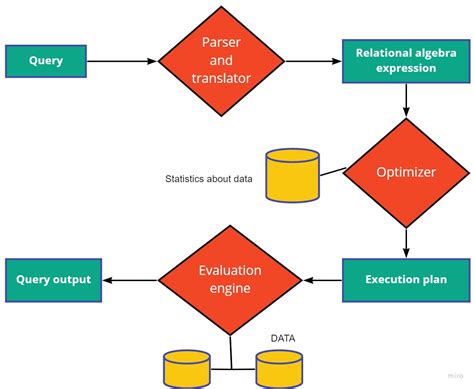
Optimizers typically work by iterating through a set of possible solutions or configurations, evaluating each one based on the objective function and constraints, and selecting the best solution or configuration that meets the optimization criteria. The process involves the following steps:
- Problem Formulation: define the optimization problem, including the objective function, constraints, and variables.
- Initialization: initialize the optimizer with a set of starting values or solutions.
- Iteration: iterate through the set of possible solutions or configurations, evaluating each one based on the objective function and constraints.
- Selection: select the best solution or configuration that meets the optimization criteria.
- Termination: terminate the optimization process when a stopping criterion is met, such as a maximum number of iterations or a satisfactory solution.
| Optimizer Type | Description |
|---|---|
| Gradient-Based Optimizers | use gradient information to search for the optimal solution |
| Derivative-Free Optimizers | do not require gradient information to search for the optimal solution |
| Population-Based Optimizers | use a population of candidate solutions to search for the optimal solution |

Applications of Optimizers
Optimizers have numerous applications in various fields, including:
- Computer Science: optimization of algorithms, data structures, and software systems.
- Engineering: optimization of systems, processes, and designs, such as structural optimization, mechanical optimization, and electrical optimization.
- Economics: optimization of economic systems, such as resource allocation, production planning, and portfolio optimization.
- Mathematics: optimization of mathematical models, such as linear programming, non-linear programming, and dynamic programming.
Key Points
- Optimizers are used to improve the performance, efficiency, or effectiveness of a particular task, process, or system.
- There are several types of optimizers, including linear programming, non-linear programming, integer programming, dynamic programming, and stochastic optimizers.
- Optimizers work by iterating through a set of possible solutions or configurations, evaluating each one based on the objective function and constraints, and selecting the best solution or configuration that meets the optimization criteria.
- Optimizers have numerous applications in various fields, including computer science, engineering, economics, and mathematics.
- The choice of optimizer depends on the specific problem characteristics, such as the number of variables, constraints, and the objective function.
Optimizers are powerful tools that can help solve complex problems and improve the performance of various systems and processes. By understanding how optimizers work and their applications, we can harness their potential to make better decisions and create more efficient systems.
What is the purpose of an optimizer?
+The purpose of an optimizer is to find the best possible solution or configuration that maximizes or minimizes a specific objective function, subject to certain constraints and limitations.
What are the different types of optimizers?
+There are several types of optimizers, including linear programming, non-linear programming, integer programming, dynamic programming, and stochastic optimizers.
How do optimizers work?
+Optimizers typically work by iterating through a set of possible solutions or configurations, evaluating each one based on the objective function and constraints, and selecting the best solution or configuration that meets the optimization criteria.

